En marzo de 1798 el matemático Joseph Fourier recibió una misteriosa citación del Ministerio del Interior de la Francia posrevolucionaria:
"Ciudadano: el directorio ejecutivo, que tiene una necesidad particular de sus talentos y de su fervor, acaba de disponer de usted por el bien del servicio público. Debe prepararse y estar listo para partir apenas reciba la orden".
Dos meses después, Fourier zarpó hacia Egipto, reclutado por Napoleón Bonaparte junto con 30.000 soldados y más de 100 académicos, pues Napoleón creía que el poder intelectual era tan importante como el poderío militar.
Y Fourier era un joven republicano que creía que los matemáticos nunca deberían olvidar su papel como sirvientes de la revolución francesa.
Para él, el valor real de las matemáticas era su utilidad para la sociedad. Y su innovadora Teoría del Calor efectivamente resultó ser muy útil: condujo a una nueva forma de entender no solo el calor, sino también la luz y el sonido.

Innoble
Joseph Fourier, el hijo huérfano de un sastre, descubrió el mágico mundo de las matemáticas cuando era un adolescente.
En su internado militar, recogía cabos de velas para poder estudiar en la noche mientras los otros niños roncaban.
Sabía que era bueno, y se comparaba con los mejores:
"Ayer cumplí 21 años; a esa edad Pascal y Newton ya habían alcanzado varias veces la inmortalidad", señaló.
Quiso unirse al ejército, pero su solicitud fue denegada.
"Fourier, por no ser noble, no puede ingresar a la artillería así sea el mejor después de Newton".
Pero la revolución francesa de 1789 —que él apoyó— cambió todo.
La aritmética republicana

La nueva república en Francia fundó nuevos centros de aprendizaje para cultivar a los nuevos pensadores de esa era revolucionaria; algunos incluso tenían su propio uniforme militar.
El único criterio para elegir a los estudiantes era la inteligencia y el conocimiento. A nadie —se pensaba— se le debía negar un lugar por falta de fondos.
Y de todas las disciplinas, las matemáticas y la ciencia eran las más apreciadas.
La enseñanza de la "aritmética republicana" era elogiada.
"Ciudadano: la revolución no solo mejora nuestra moral y allana el camino para nuestra felicidad y la de las generaciones futuras, sino que además libera el progreso científico de los grilletes que lo frenan".
El talento de Fourier, no solo como matemático sino también como maestro, no pasó desapercibido.
Fue nombrado director de educación matemática en la nueva École Polytechnique, donde por primera vez fue posible recibir clases de matemáticas enseñadas por quienes las estaban creando.
Las conferencias matemáticas eran un espectáculo. Los profesores tenían que dar sus conferencias de pie, sin notas ni un escritorio tras del cual esconderse. El diálogo y el debate entre el profesor y los estudiantes era más que bienvenido.
En ese ambiente, Fourier, en particular, prosperó gracias a que tenía "una voz fuerte y es activo, ingenioso y muy erudito", según su tutor Joseph-Louis Lagrange, el matemático y astrónomo de la Era de la Ilustración italiana.
Bajo el sol del desierto

Las habilidades oratorias de Fourier, que habían sido utilizadas para defender la revolución política, fueron luego empleadas en la propagación de una revolución matemática.
Gracias a ello, Napoleón se enteró de su existencia y recibió esa misteriosa convocatoria para zarpar hacia Egipto.
Pero tras la Batalla de las Pirámides, Napoleón regresó a Francia y Fourier quedó varado en El Cairo.
En 1799, ayudó a descubrir la Piedra de Rosetta en el medio del desierto egipcio.
Fue allá donde Fourier se enamoró… del calor. No solo las matemáticas que escondía sino de los fantásticos poderes medicinales que estaba convencido que tenía.
Cuando regresó, sus amigos lo encontraron sentado en su habitación sobrecalentada en Grenoble, en el sur de Francia, envuelto como una momia egipcia, sudando, y pensando cómo explicar exactamente cómo se mueve el calor a través del espacio.

¿Cómo se mueve el calor de un sitio al otro?
Incluso antes de responder a la pregunta que él mismo se había planteado, Fourier anticipó cuán importante sería la respuesta, no solo para comprender el calor, sino para toda la física:
"El calor, como la gravedad, penetra en todas las sustancias del Universo, sus rayos ocupan todas las partes del espacio. El objetivo de nuestro trabajo es establecer las leyes matemáticas a las que este elemento obedece. La teoría del calor formará a partir de ahora una de las ramas más importantes de la física general".
Su predicción fue acertada.
La comprensión matemática de Fourier de cómo se mueve el calor nos ha permitido comprender cualquier cosa que pueda describirse como una onda, como el sonido y la luz.
La gran idea de Fourier fue que cada onda, por compleja que fuera, podía explicarse como la suma de muchas ondas sinusoidales.
Las ondas sinusoidales son las ondas más simples que existen: si las dibujas en un papel, son una serie de curvas suaves, regulares, que suben y bajan.
Y la onda de sonido más simple que existe es el sonido puro de un diapasón.

El sonido de una trompeta, por ejemplo, es más complicado.
La forma de sus ondas se parece al borde de sierra o una cadena montañosa con innumerables picos de diferentes inclinaciones y alturas.
Fourier creía que si podía entender a fondo todas estas diferentes formas de onda, si de alguna manera pudiera relacionarlas, una con otra, descubriría algo importante. Estaba buscando los principios subyacentes que determinan sus muchas formas diversas.
Y su revelación fue esta: cada forma de onda, sin importar cuán complicada y abigarrada, se puede dividir en un conjunto básico de ondas sinusoidales simples y lisas.
O, dicho de otra manera, si uno "suma" muchas ondas sinusoidales simples de diferentes frecuencias (es decir, curvas con los baches más o menos montados juntos) puede reproducir el perfil irregular de la onda de la trompeta.
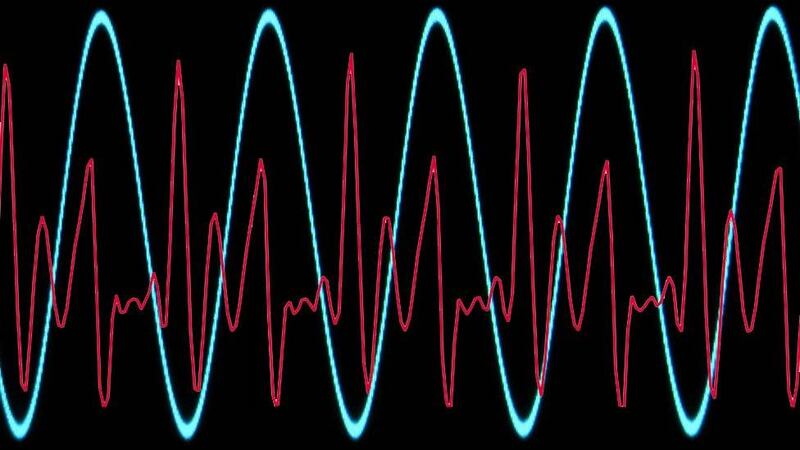
De eso se trataba la pionera Teoría del Calor de Fourier: explicaba cómo se relacionan todas las ondas entre sí.
"Las matemáticas comparan los fenómenos más diversos y descubren las analogías secretas que los unen", dijo.
Su análisis es una brillante pieza de matemática pura.
¿Qué sucedió con la idea?
Cuando publicó por primera vez su Teoría Analítica del Calor, se encontró con una fuerte oposición.
Muchos colegas académicos se mostraron escépticos. Les parecía imposible que las ondas sinusoidales lisas pudieran llegar a producir ondas complicadas, filodentadas como, por ejemplo, las de una trompeta.
Pero Fourier continuó trabajando en su tratado hasta que publicó la versión final en 1822.
Pasó tiempo antes de que los logros de Fourier fueran reconocidos, pero cuando lo fueron, no hubo quien frenara las alabanzas.
Uno de los más respetados físicos, Lord Kelvin, cuyo nombre se usó para nombrar la unidad científica moderna de la temperatura, declaró:
"El de Fourier no solo es uno de los más bellos resultados del análisis moderno, sino que además proporciona un instrumento indispensable en el tratamiento de casi todas las preguntas recónditas en la física moderna. Fourier es un poema matemático".

Como predijo Fourier, su teoría formó una de las ramas más importantes de la física general.
No solo abarca cualquier fenómeno que pueda describirse como una onda sino que nos da una forma de pensar acerca de estos fenómenos del mundo muy real.
Es la razón por la que funciona tu radio o tu reproductor de música, entre otras cosas.
Los algoritmos sencillamente le dicen al altavoz que vibre para crear todas las ondas simples sinusoidales que componen un sonido particular. Al sonar simultáneamente, estas ondas simples pueden recrear milagrosamente toda una orquesta.
Su investigación sobre ese calor que lo cautivó en el desierto egipcio condujo a una de las ideas matemáticas más potentes de todos los tiempos —la gramática de las formas de onda— confirmando una de sus creencias:
"El estudio profundo de la naturaleza es la fuente más fértil de descubrimientos matemáticos".
Ahora puedes recibir notificaciones de BBC News Mundo. Descarga la nueva versión de nuestra app y actívalas para no perderte nuestro mejor contenido.

